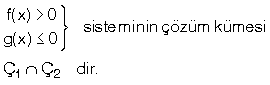A. TANIM f(x) > 0, f(x) < 0, f(x) ³ 0, f(x) £ 0 ifadelerine fonksiyonların eşitsizliği denir.
Bu eşitsizlikleri sağlayan sayıların oluşturduğu kümeye de eşitsizliğin çözüm kümesi denir.
B. BİRİNCİ DERECEDEN BİR BİLİNMEYENLİ EŞİTSİZLİKLER
m # 0 olmak üzere, f(x) = mx + n koşulunu sağlayan noktalar analitik düzlemde bir doğru belirtir.


C. İKİNCİ DERECEDEN BİR BİLİNMEYENLİ EŞİTSİZLİKLER
f(x) = ax2 + bx + c koşulunu sağlayan noktalar analitik düzlemde bir parabol belirtir.
1) D > 0 ise,


2) D = 0 ise,


3) D < 0 ise,


1. f(x) = ax2 + bx + c > 0 ın çözüm kümesi bütün gerçel sayılar ise,
D < 0 ve a > 0 dır.
2. f(x) = ax2 + bx + c < 0 ın çözüm kümesi bütün gerçel sayılar ise,
D < 0 ve a < 0 dır.
3. a < 0 ve D < 0 ise,
f(x) = ax2 + bx + c > 0 ın çözüm kümesi boş kümedir.
* Polinom fonksiyonlarından oluşan rasyonel fonksiyonların eşitsizliği incelenirken aşağıdaki 5 adım izlenerek çözüm kümesi bulunur. Bu, bütün eşitsizliklerde uygulanabilen pratik bir çözüm yoludur.
1. Adım : Verilen ifadedeki her çarpan ayrı ayrı sıfıra eşitlenerek kökler bulunur.
2. Adım : Bulunan bu kökler sayı doğrusunda sıralanır.
3. Adım : Sistemin işareti bulunur.
4. Adım : Bulunan bu işaret, tablonun en sağındaki kutuya yazılır.
5. Adım : Tablodaki diğer kutular sırayla sola doğru doldurulur.
* Çift katlı köklerde grafik Ox eksenine teğet olduğundan eğri, o noktada da işaret değiştirmez.

(x + 1)100 = 0 ise x = 1 çift katlı köktür.
(x 1)99 = 0 ise x = 1 tek katlı köktür.
* çözüm kümesine;
çözüm kümesine;
P(x) = 0 ı sağlayan x değerleri alınır,
Q(x) = 0 ı sağlayan x değerleri alınmaz.
Bu eşitsizlikleri sağlayan sayıların oluşturduğu kümeye de eşitsizliğin çözüm kümesi denir.
B. BİRİNCİ DERECEDEN BİR BİLİNMEYENLİ EŞİTSİZLİKLER
m # 0 olmak üzere, f(x) = mx + n koşulunu sağlayan noktalar analitik düzlemde bir doğru belirtir.


C. İKİNCİ DERECEDEN BİR BİLİNMEYENLİ EŞİTSİZLİKLER
f(x) = ax2 + bx + c koşulunu sağlayan noktalar analitik düzlemde bir parabol belirtir.
1) D > 0 ise,


2) D = 0 ise,


3) D < 0 ise,


1. f(x) = ax2 + bx + c > 0 ın çözüm kümesi bütün gerçel sayılar ise,
D < 0 ve a > 0 dır.
2. f(x) = ax2 + bx + c < 0 ın çözüm kümesi bütün gerçel sayılar ise,
D < 0 ve a < 0 dır.
3. a < 0 ve D < 0 ise,
f(x) = ax2 + bx + c > 0 ın çözüm kümesi boş kümedir.
* Polinom fonksiyonlarından oluşan rasyonel fonksiyonların eşitsizliği incelenirken aşağıdaki 5 adım izlenerek çözüm kümesi bulunur. Bu, bütün eşitsizliklerde uygulanabilen pratik bir çözüm yoludur.
1. Adım : Verilen ifadedeki her çarpan ayrı ayrı sıfıra eşitlenerek kökler bulunur.
2. Adım : Bulunan bu kökler sayı doğrusunda sıralanır.
3. Adım : Sistemin işareti bulunur.
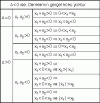
Sistemin işareti; her çarpandaki en büyük dereceli değişkenlerin katsayılarının çarpımının işaretidir.
4. Adım : Bulunan bu işaret, tablonun en sağındaki kutuya yazılır.
5. Adım : Tablodaki diğer kutular sırayla sola doğru doldurulur.
Tek katlı kökün soluna sağındaki işaretin zıttı, çift katlı kökün soluna sağındaki işaretin aynısı yazılır.
* Çift katlı köklerde grafik Ox eksenine teğet olduğundan eğri, o noktada da işaret değiştirmez.

(x + 1)100 = 0 ise x = 1 çift katlı köktür.
(x 1)99 = 0 ise x = 1 tek katlı köktür.
*
P(x) = 0 ı sağlayan x değerleri alınır,
Q(x) = 0 ı sağlayan x değerleri alınmaz.