Yansıma ile dönme birbirinden farklıdır.
Yansımada; gerçek şekle ve görüntüsüne ( yansımasına ) baktığımız zaman birbirlerine ters dururlar.
Yani sağda olan solda, solda olan sağdadır.
Fakat dönme hareketinde sağda olan hep sağda,solda olan kısım da hep solda durur.
Dönme hareketine en iyi örnek çarkıfelektir.
Çarkıfelek ne kadar dönerse dönsün sayıların sıralanışı değişmez.
Dönme hareketi genellikle 90 ,180 veya 270 derece olarak yapılır.
360 derece pek karşımıza çıkmaz,zaten 360 derece dönmesi demek, cismin olduğu yerde kalması demektir.
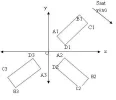
Örnek: Şimdi elimizde A(-3,+2) noktası olsun, bu noktayı 90 derece saat yönünde döndürelim. Döndükten sonraki oluşan A şeklinin yeni haline A1 dersek,
A1 in koordinatları = A1(+2,+3) olacaktır.
Peki yukarıda neler oldu buna bakalım.
Her 90 derece dönmede noktaların koordinatları yer değişir ve ikinci koordinatın işareti - ile çarpılır.
Burada da A(-3,+2) noktasını 90 derece döndürdüğümüzde ne oldu?
Koordinatlar yer değişti yani A1(+2,-3) oldu, devamında ise ikincinin işaretini - ile çarptık.
Yani tam sonuç A1(+2,+3) elde edildi.
Sonuç: Bir noktayı saat yönünde 90 derece çevirdiğimizde noktanın koordinarları önceden A(a,b) ise dönme sonrası A1(b,-a) elde edilir.
180 derece sorulduğunda bu işlem 2 kere tekrar edilir, 270 derece sorulduğunda 3 kere tekrar edilir.
Yukarıda;
A1(+2,+3) , B1(+6,+6) , C1(+7,+5), D1(+3,+1) noktalarının köşesinde olduğu bir dikdörtgen saat yönünde önce 90, sonra bir daha 90 derece döndürülmektedir. Yani ikinci dönmede baştakine göre şeklimiz 180 derece dönmüştür.
O halde ilk 90 derece dönmede yukarıdaki kuralımıza göre:
A2(+3,-2), B2(+6,-6), C2(+5,-7), D2(+1,-3) elde edilir.
Bunları bir daha 90 derece döndürürsek, baştakine göre 180 derece döndürmüş oluruz ve 3. şekil elde edilir.
Onun koordinatlarını da siz bulmaya çalışın.
* Peki saat yönünün tersine döndürüldüğünü düşünelim.
Örnek: A(+2,-3) noktasının saat yönünün tersine 90 derece dönmesiyle oluşan yeni koordinatı nedir?
Çözüm: Tersten düşünelim. Elimizdeki şeklin 90 derece ters yöne dönmesini bulacağız, o halde şu anki A(+2,-3) noktası bulacağımız şeklin saat yönüne dönmüş halidir.
Tersten bakarsak;
A(+2,-3) hangi koordinatın saat yönünde dönmüş hali olabilir?
A2(+3,+2) imiş ki saat yönünde dönünce A(+2,-3) elde edilmiş.
O halde;
Sonuç: Noktalar aat yönünün tersine döndürülecek olursa, A(a,b) olan koordinatı A2(-b,a) olarak değişmektedir.
Öteleme ve yansıma:
öteleme: bir cismin duruşunun değişmeden sadece yer değişmesidir.
Yansıma ise cismin duruşunun belirli bir yere göre ters dönmesidir.
Öteleme ve yansıma farklı şeylerdir.
Fakat bazı şekilleri ötelesek de yansıma yapsak da aynı şekil elde edilir.
Örneğin: T harfinin aynadaki yansıması yine T şeklindedir. T harfinin ötelemesi de T şeklindedir.
Yani T harfinin ötelenmiş ve yansımış şekli aynıdır.
Buna ötelemeli yansıma (öteleme simetrisi) denir.
Bunun haricinde: Cisimleri önce öteleyip sonra yansıma yapmakla,
önce yansıma yapıp sonra öteleyerek elde edilen sonuçlar değişmez.
istenen sırayla gidilebilir.
Kendiniz de bu örnekleri çoğaltabilirsiniz.
Öteleme nedir?
Bir nesnenin bir yerden başka bir yere belirli bir doğrultu ve yönde (sağ, sol, yukarı, aşağı) yaptığı kayma hareketine öteleme denir. Öteleme hareketi sonunda nesnenin geldiği yer, görüntüsüdür.
Ötelemede şeklin duruşu, biçimi ve boyutları aynı kalır.
Örneğin şeklimiz 3 birim yukarı, 4 birim sağa kaydırılacak ama yönü değişmeyecek sadece yer değiştirmiş olacak.
Yansımada; gerçek şekle ve görüntüsüne ( yansımasına ) baktığımız zaman birbirlerine ters dururlar.
Yani sağda olan solda, solda olan sağdadır.
Fakat dönme hareketinde sağda olan hep sağda,solda olan kısım da hep solda durur.
Dönme hareketine en iyi örnek çarkıfelektir.
Çarkıfelek ne kadar dönerse dönsün sayıların sıralanışı değişmez.
Dönme hareketi genellikle 90 ,180 veya 270 derece olarak yapılır.
360 derece pek karşımıza çıkmaz,zaten 360 derece dönmesi demek, cismin olduğu yerde kalması demektir.
Örnek: Şimdi elimizde A(-3,+2) noktası olsun, bu noktayı 90 derece saat yönünde döndürelim. Döndükten sonraki oluşan A şeklinin yeni haline A1 dersek,
A1 in koordinatları = A1(+2,+3) olacaktır.
Peki yukarıda neler oldu buna bakalım.
Her 90 derece dönmede noktaların koordinatları yer değişir ve ikinci koordinatın işareti - ile çarpılır.
Burada da A(-3,+2) noktasını 90 derece döndürdüğümüzde ne oldu?
Koordinatlar yer değişti yani A1(+2,-3) oldu, devamında ise ikincinin işaretini - ile çarptık.
Yani tam sonuç A1(+2,+3) elde edildi.
Sonuç: Bir noktayı saat yönünde 90 derece çevirdiğimizde noktanın koordinarları önceden A(a,b) ise dönme sonrası A1(b,-a) elde edilir.
180 derece sorulduğunda bu işlem 2 kere tekrar edilir, 270 derece sorulduğunda 3 kere tekrar edilir.
Yukarıda;
A1(+2,+3) , B1(+6,+6) , C1(+7,+5), D1(+3,+1) noktalarının köşesinde olduğu bir dikdörtgen saat yönünde önce 90, sonra bir daha 90 derece döndürülmektedir. Yani ikinci dönmede baştakine göre şeklimiz 180 derece dönmüştür.
O halde ilk 90 derece dönmede yukarıdaki kuralımıza göre:
A2(+3,-2), B2(+6,-6), C2(+5,-7), D2(+1,-3) elde edilir.
Bunları bir daha 90 derece döndürürsek, baştakine göre 180 derece döndürmüş oluruz ve 3. şekil elde edilir.
Onun koordinatlarını da siz bulmaya çalışın.
* Peki saat yönünün tersine döndürüldüğünü düşünelim.
Örnek: A(+2,-3) noktasının saat yönünün tersine 90 derece dönmesiyle oluşan yeni koordinatı nedir?
Çözüm: Tersten düşünelim. Elimizdeki şeklin 90 derece ters yöne dönmesini bulacağız, o halde şu anki A(+2,-3) noktası bulacağımız şeklin saat yönüne dönmüş halidir.
Tersten bakarsak;
A(+2,-3) hangi koordinatın saat yönünde dönmüş hali olabilir?
A2(+3,+2) imiş ki saat yönünde dönünce A(+2,-3) elde edilmiş.
O halde;
Sonuç: Noktalar aat yönünün tersine döndürülecek olursa, A(a,b) olan koordinatı A2(-b,a) olarak değişmektedir.
Öteleme ve yansıma:
öteleme: bir cismin duruşunun değişmeden sadece yer değişmesidir.
Yansıma ise cismin duruşunun belirli bir yere göre ters dönmesidir.
Öteleme ve yansıma farklı şeylerdir.
Fakat bazı şekilleri ötelesek de yansıma yapsak da aynı şekil elde edilir.
Örneğin: T harfinin aynadaki yansıması yine T şeklindedir. T harfinin ötelemesi de T şeklindedir.
Yani T harfinin ötelenmiş ve yansımış şekli aynıdır.
Buna ötelemeli yansıma (öteleme simetrisi) denir.
Bunun haricinde: Cisimleri önce öteleyip sonra yansıma yapmakla,
önce yansıma yapıp sonra öteleyerek elde edilen sonuçlar değişmez.
istenen sırayla gidilebilir.
Kendiniz de bu örnekleri çoğaltabilirsiniz.
Öteleme nedir?
Bir nesnenin bir yerden başka bir yere belirli bir doğrultu ve yönde (sağ, sol, yukarı, aşağı) yaptığı kayma hareketine öteleme denir. Öteleme hareketi sonunda nesnenin geldiği yer, görüntüsüdür.
Ötelemede şeklin duruşu, biçimi ve boyutları aynı kalır.
Örneğin şeklimiz 3 birim yukarı, 4 birim sağa kaydırılacak ama yönü değişmeyecek sadece yer değiştirmiş olacak.