Üçgende metrik bağıntılar

İKİZKENAR ÜÇGEN​

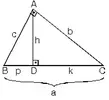
1. İkizkenar üçgenin tepe açısından tabanına çizilen yükseklik, hem açıortay, hem de kenarortaydır.


2. Bir üçgende, açıortay aynı zamanda yükseklik ise bu üçgen ikizkenar üçgendir.
|AB| = |AC| |BH| = |HC|m(B) = m(C)


3. Bir üçgende, yükseklik aynı zamanda kenarortay ise bu üçgen ikizkenar üçgendir.
|AB| = |AC| m(BAH) = m(HAC)m(B) = m(C)

İkizkenar üçgende açıortay, kenarortay ve yüksekliğin aynı olması birçok yerde karşımıza çıktığından çok iyi bilinmesi gereken bir özelliktir.

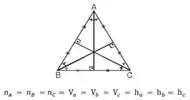
4. İkizkenar üçgende ikizkenara ait yükseklikler eşittir. Bu durumda yüksekliklerin kesim noktasının ayırdığı parçalarda eşit olur.


5. İkizkenar üçgende ikizkenara ait kenarortaylar ve kenarortayların kesim noktasının ayırdığı parçalar da birbirine eşittir.


6. İkizkenar üçgende eşit açılara ait açıortaylar da eşittir. Açıortaylar birbirini aynı oranda bölerler.


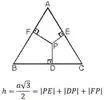
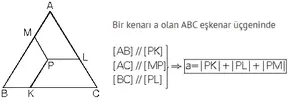
7. İkizkenar üçgende ikiz olmayan kenar üzerindeki herhangi bir noktadan ikiz kenarlara çizilen dikmelerin toplamı, ikizkenarlara ait yüksekliği verir.

Eşkenar Üçgen​

Tüm kenar uzunlukları eşit olan üçgene eşkenar üçgen denir. İç açıları da birbirine eşit ve her biri 60 derecedir.

Eşkenar Üçgen Özellikleri​

• İç açılar toplamı 180 derecedir.
• Her bir açısı 60 derecedir.
• Kenar uzunlukları birbirine eşittir.
• Eşkenar üçgende bütün açıortay, kenarortay, yükseklikler, çakışık ve hepsinin uzunlukları eşittir.
• Bir kenara ait yükseklik, aynı zamanda o kenara ait açıortay, kenarortay ve orta dikmedir.
• Eşkenar üçgenin içindeki herhangi bir noktadan kenarlara çizilen dik uzunlukların toplamı eşkenar üçgene ait yüksekliği verir.
• Eşkenar üçgenin içindeki herhangi bir noktadan kenarlara çizilen paralellerin uzunluklarının toplamı bir kenar uzunluğuna eşittir.
• Eşkenar üçgen ikizkenar üçgenin tüm özelliklerini taşır.
• Eşkenar üçgenin tüm merkezleri (diklik merkezi, iç teğet çemberin merkezi, ağırlık merkezi, çevrel çemberin merkezi) aynı noktadadır.

Eşkenar Üçgeni detaylıca inceleyelim​

Eşkenar üçgende bütün açıortay, kenarortay yükseklikler çakışık ve hepsinin uzunlukları eşittir.


Eşkenar üçgenin içindeki herhangi bir noktadan kenarlara çizilen dik uzunlukların toplamı, eşkenar üçgene ait yüksekliği verir. Bir kenarı a olan eşkenar üçgende;


Eşkenar üçgenin içindeki herhangi bir noktadan kenarlara çizilen paralellerin toplamı bir kenar uzunluğuna eşittir.

Dik Üçgen​

Dik üçgen, iç açılarından biri 90° olan üçgendir. Çemberde çapı gören çevre açı 90°’dir.

Dik Üçgen Özellikleri​

• Bir açısı 90 derecedir.
• İç açılarının toplamı 180 derecedir.
• Dik üçgenin diklik merkezi (yüksekliklerin kesişim noktası) dik kenarların kesiştiği köşededir.
• Dik üçgenin orta dikmelerinin kesişim noktası hipotenüsün orta noktasıdır.
• Dik üçgenler çeşitkenar ya da ikizkenar olabilir ancak eşkenar olamaz.
• Dik üçgenin dik olmayan iki açısı dar ve tümler açılardır.
• Dik üçgende dik açının gördüğü kenara hipotenüs adı verilir ve dik üçgenin en uzun kenarıdır.

Pisagor Bağıntısı Nedir?​

Bir dik üçgende hipotenüsün uzunluğunun karesi dik kenarların kareleri toplamına eşittir.

Hipotenüsün karesi = Dik kenarların kareleri toplamı

x² + y² = z²

ÖKLİT BAĞINTILARI​

Dik üçgenlerde hipotenüse ait yüksekliğin verildiği durumlarda benzerlikten kaynaklanan öklit bağıntıları kullanılır.



1. Yüksekliğin hipotenüste ayırdığı parçaların çarpımı yüksekliğin karesine eşittir.

h2 = p.k
c2 = p.a
b2 = k.a

2. ABC üçgeninin alanını iki farklı şekilde yazıp eşitlediğimizde

a.h =b.c

* Yukarıda anlatılan öklit bağıntıları kullanılarak elde edilir.

Genellikle bu öklit bağıntısını kullanmak yerine, yukarıdaki öklit bağıntıları ve pisagor bağıntısını kullanarak çözüme gideriz.

Doğru bir tespit, ikizkenar üçgenlerde her tepe açıdan taban kenarına çizilen yükseklik hem açıortay hem de kenarortaydır. Bu durum üçgende bazı özel açı eşitliklerini de beraberinde getirir. İkizkenar üçgenler oldukça ilginç özelliklere sahiptir.