Kutupsal Koordinat sistemi

Suskun

V.I.P

V.I.P

• 2 Ock 2010

• #1

Kutupsal Koordinat sistemi

Konu başlıkları


Tarihçesi
Kutupsal koordinatlar ile noktaların belirtilmesi
Radyan ölçüsünün kullanımı
Kutupsal ve kartezyen koordinatlar arası dönüşüm
Kutupsal denklemler
Çember
Doğru
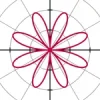
Kutupsal gül
Arşimet spirali
Konik kesitler
Diğer eğriler
calculus(analiz)
Diferansiyel hesaplama
İntegral hesaplama
Vektörel hesaplamalar
Üç boyut
Silindirik koordinatlar
Küresel koordinatlar
Uygulamalar
Robot bilimi
Havacılık
Arşimet spirali
Kepler'in gezegensel hareket kanunları

​

Matematikte kutupsal koordinat sistemi veya polar koordinat sistemi, noktaların birer açı ve Kartezyen koordinat sistemindeki orijinin eşdeğeri olup "kutup" olarak bilinen bir merkez noktaya olan uzaklıklar ile tanımlandığı, iki boyutlu bir koordinat sistemidir. Kutupsal koordinat sistemi, matematik, fizik, mühendislik, denizcilik, robot teknolojisi gibi birçok alanda kullanılır. Bu sistem, iki nokta arasındaki ilişkinin açı ve uzaklık ile daha kolay ifade edilebildiği durumlar için özellikle kullanışlıdır. Kartezyen koordinat sisteminde, böyle bir ilişki ancak trigonometrik formüller ile bulunabilir. Kutupsal denklemler, çoğu eğri tipi için en kolay, bazıları içinse yegâne tanımlama yöntemidir.


Tarihçesi
Antik Yunan uygarlığı'nda açı ve yarıçap kavramlarının kullanıldığı bilinmektedir. (MÖ 190 - 120), her açı için kiriş uzunluklarını veren bir kiriş fonksiyonları tablosu oluşturmuştur ve yıldızların konumlarını belirlemek için kutupsal koordinatlar kullandığına ilişkin kaynaklar bulunmaktadır. "Spiraller Üzerine" (On Spirals) adlı eserinde Arşimet, ünlü spiralini yarıçapın açıya bağlı olduğu bir fonksiyon olarak tanımlar. Bununla beraber, Yunan çalışmaları, koordinat sistemini tam olarak tanımlayamamıştır.

Kutupsal koordinatları resmî bir koordinat sisteminin parçası olarak ilk olarak kimin tanımladığına ilişkin farklı söylemler vardır. Konunun tarihçesi, Harvard profesörü Julian Lowell Coolidge'in "Kutupsal Koordinatların Kaynağı" (Origin of Polar Coordinates) adlı kitabında anlatılmıştır. Grégoire de Saint-Vincent ve Bonaventura Cavalieri yaklaşık aynı zamanda birbirinden bağımsız olarak kavramları oluşturmaya başlamıştır. Saint-Vincent, çalışmalarını 1625 yılında yazmış ve 1647 yılında yayınlamışken, Cavalieri de 1635 yılında kendi çalışmalarının ilk baskısını yapıp, 1653 yılında elden geçirilmiş bir sürümünü yayınlamıştır. Bir Arşimet spirali içindeki alanla ilgili bir problemin çözümünde kutupsal koordinat sisteminden ilk yararlanan Cavalieri olmuştur. Daha sonra Blaise Pascal, parabolik yayların uzunluğunu hesaplamak için kutupsal koordinatları kullanmıştır.

1671 yılında yazılmış ve 1736 yılında basılmış olan Method of Fluxions çalışmasıyla Isaac Newton, kutupsal koordinatlara bir düzlemdeki herhangi bir noktanın yerini saptama yöntemi olarak bakan ilk kişi olmuştur. Newton, kutupsal koordinatlar ve diğer dokuz koordinat sistemi arasındaki dönüşümleri incelemiştir. Acta eruditorum (1691) adlı çalışmasında Jacob Bernoulli, sırasıyla kutup ve kutupsal eksen olarak adlandırdığı bir nokta ve o noktanın üzerinde yer aldığı eksenden oluşan bir sistem kullanmıştır. Bu sistemde koordinatlar, kutba göre uzaklık ve kutup eksenine göre açı ile belirtilmiştir. Bernoulli'nin çalışması, bu koordinatlarla tanımlanmış eğrilerin eğim yarıçaplarını hesaplamaya kadar ilerlemiştir.

Gregorio Fontana'ya atfedilmiş olan kutupsal koordinatlar terimi, 18. yüzyıl İtalyan yazarları tarafından kullanılmıştır. Terimin İngilizce yayınlarda ilk yer alışı, George Peacock'ın Sylvestre François Lacroix'ya ait "Diferansiyel ve İntegral Hesaplamalar" (Differential and Integral Calculus) adlı kitabını çevirmesi ile 1816 yılında olmuştur.
Alexis Clairaut ve Leonhard Euler, kutupsal koordinat kavramının üç boyuta uyarlanmasında rol oynamışlardır.

 

Suskun

V.I.P

V.I.P

• 2 Ock 2010

• #2

Kutupsal koordinatlar ile noktaların belirtilmesi

(3, 60°) ve (4, 210°) noktaları

Tüm iki boyutlu koordinat sistemlerinde olduğu gibi, kutupsal koordinat sisteminde de iki koordinat vardır: r ("radyal koordinat" ya da "ışınsal koordinat") ve θ ("açısal koordinat", "kutupsal açı" ya da "yatay açı" ; bazen φ veya t ile gösterilir). r koordinatı, kutuptan olan ışınsal uzaklığı; θ koordinatı ise noktanın üzerinde bulunduğu ışının, bazen "kutupsal eksen" de denilen 0° ışınından saat yönünün tersi yönündeki açısını ifade eder. 0° ışını, Kartezyen koordinat sisteminde "pozitif x ekseni" olarak bilinir.olmakla beraber olmamakdatır

Örneğin, kutupsal koordinatları (3, 60°) olan bir nokta, kutupsal eksene 60° açı ile duran ışın üzerinde kutuptan 3 birim uzaklıkta bulunur. Koordinatları (-3, 240°) olan nokta da aynı yerde gösterilecektir çünkü bir negatif ışınsal uzaklık, karşıt ışın üzerinde pozitif uzaklık olarak ölçülür (240° − 180° = 60°).

Kutupsal koordinat sisteminin Kartezyen koordinat sisteminde bulunmayan bir önemli özelliği, belli bir noktanın sonsuz sayıda farklı koordinat ile belirtilebilmesidir. Genel olarak, n herhangi bir tam sayı olmak üzere, herhangi bir (r, θ) noktası (r, θ ± n×360°) veya (−r, θ ± (2n + 1)180°) olarak gösterilebilir.[8] Eğer bir noktanın r koordinatı 0 ise, o nokta θ koordinatından bağımsız olarak kutup üzerinde bulunur.

 

Suskun

V.I.P

V.I.P

• 2 Ock 2010

• #3

Kutupsal ve kartezyen koordinatlar arası dönüşüm

Kutupsal koordinatlar r ve θ, kartezyen koordinatlara şu şekilde dönüştürülebilir.






Bu iki formüle göre x ve y cinsinden elde edilen dönüşüm formülleri ise şöyledir:




Eğer x = 0 ve

* y pozitifse, θ = 90° (π/2 rad);
* y negatifse, θ = 270° (3π/2 rad) olur.

 

Suskun

V.I.P

V.I.P

• 2 Ock 2010

• #4

Kutupsal denklemler

Kutupsal koordinatlar ile ifade edilmiş bir eğri denklemi "kutupsal denklem" olarak bilinir ve genellikle r, θ'nın bir fonksiyonu olarak yazılır.

Kutupsal denklemler değişik simetri biçimleri gösterebilir. Bir eğri,

* eğer r(−θ) = r(θ) ise 0°/180° yatay ışınına göre,
* eğer r(π−θ) = r(θ) ise 90°/270° dikey ışınına göre ve
* eğer r(θ−α) = r(θ) ise saat yönünün tersinde, rotasyonel (dönel) olarak kutup noktasına göre α° kadar simetrik olacaktır.

 

Suskun

V.I.P

V.I.P

• 2 Ock 2010

• #5

Çember



Merkezi (r0, φ) noktasında ve yarıçapı a olan herhangi bir çemberin genel denklemi şu şekildedir:



Bu denklem özel durumlar için çeşitli yollarla basitleştirilebilir. Örneğin



merkezi kutup noktasında ve yarıçapı a olan çember için yazılmış denklemdir

 

Suskun

V.I.P

V.I.P

• 2 Ock 2010

• #6

Doğru

Kutuptan geçen ışınsal doğrular şu denklemle gösterilir:



Burada φ, doğrunun eğim açısıdır ve m'nin Kartezyen koordinat sistemindeki eğimi temsil ettiği



denklemi ile de ifade edilebilir.

Kutup noktasından geçmeyen herhangi bir doğru, ışınsal bir doğruya diktir.[12] θ = φ doğrusunu (r0, φ) noktasında dik kesen doğrunun denklemi ise şöyledir:

 

Suskun

V.I.P

V.I.P

• 2 Ock 2010

• #7

Kutupsal gül



r(θ) = 2 sin 4θ denklemi ile verilmiş kutupsal gül şekli.
Kutupsal gül, taç yapraklı bir çiçeği andıran ve sadece kutupsal bir denklem ile ifade edilebilen ünlü bir matematiksel eğridir. Şu denklemlerle tanımlanır:

 

Suskun

V.I.P

V.I.P

• 2 Ock 2010

• #8

Arşimet spirali




Arşimet spirali, Arşimet tarafından keşfedilmiş ve gene yalnızca bir kutupsal denklem ile tanımlanabilen, ünlü bir spiraldir. Şu denklemle ifade edilir:



a değişkeninin değişimi spirali döndürürken, b değişkeni spiralin kolları arasındaki daima sabit olan uzaklığı kontrol eder. Arşimet spirali, θ > 0 ve θ < 0 değerleri için iki kola sahiptir. İki kol kutup noktasında birbirine düzgün biçimde bağlanır. Kollardan birinin 90°/270° doğrusu üzerinden ayna simetrisi alınırsa, diğer kol elde edilir.

 

Suskun

V.I.P

V.I.P

• 2 Ock 2010

• #9

Konik kesitler



Semi-latus rectum mesafesinin gösterildiği bir elips
Büyük ekseni kutupsal eksen (0° ışını) üzerinde, bir odağı kutup noktasında ve diğer odağı da kutupsal eksen üzerindeki başka bir noktada bulunan bir konik kesit şu kutupsal denklem ile tanımlanır:



Burada e eksantriklik ve l de (semi-latus rectum) büyük eksene dik olarak bir odaktan eğriye kadar ölçülen uzaklıktır. Denklem; e > 1 ise bir hiperbol, e = 1 ise bir parabol ve e < 1 ise bir elips oluşturur. e < 1 koşulunun özel bir durumu olarak e = 0 ise, yarıçapı l olan bir çember

 

Suskun

V.I.P

V.I.P

• 2 Ock 2010

• #10

Diğer eğriler
Kutupsal koordinat sisteminin dairesel özelliği, birçok eğrinin Kartezyen biçimdense kutupsal bir denklemle çok daha kolay tanımlanmasını sağlar. Bu eğrilerin arasında lemniskatlar, ilmek eğrileri (limaçonlar) ve özel bir tip limaçon olan kardiyoidler vardır.

calculus
Kutupsal koordinatlar ile ifade edilmiş denklemlere kalkulus (diferansiyel ve integral hesaplamalar) uygulanabilir.

Diferansiyel hesaplama
Bir r(θ) kutupsal eğrisine herhangi bir noktasından teğet olan doğrunun Kartezyen eğimini bulmak için, eğri öncelikle parametrelere bağlı bir denklem sistemi ile tanımlanır:




Sonra, bu denklemlerin θ'ya göre türevlerinin alınmasıyla şu denklemler elde edilir:



Birinci denklemin ikinciyle bölünmesi sonucunda da eğriye (r, r(θ)) noktasında teğet olan doğrunun Kartezyen eğimine ait denklem elde edilir: